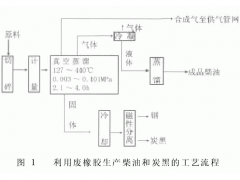
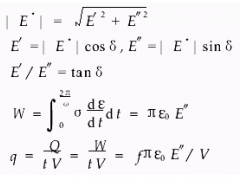姚岐軒 (曙光橡膠工業研究設計院,廣西桂林541004) 編譯
0 前言
用共聚單體含量較高的乙烯-辛烯為基礎的共聚物能制得高無定型低密度的產品。這些密度小于0.885的共聚物被稱為聚烯烴彈性體(POE)。由于聚烯烴彈性體結構規整,無毒性成分,用其加工成的海綿膠被用于制造緩沖膠條、墊片和密封制品等。有關新型乙烯-辛烯共聚物(嵌段共聚物,牌號Engage)硫化膠的結構與性能的關系研究業已成熟。發泡劑和沉淀法白炭黑的用量,對其結構與性能的影響已有報道。了解閉合微孔材料(橡膠/塑料)的動態力學特性對各種工程應用中進行卓有成效的設計是一個重要的基礎。
該項研究的目的是分析填充于閉孔乙烯辛烯嵌段共聚物硫化膠中的沉沉法白炭黑的動態力學特性;研究發泡劑(密度)和填充劑用量頻率和溫度對上述特性的影響。
1 試驗
1.1 材料
使用含25 wt%的辛烯單體、熔體流動指數為0.5 g/10 min、密度為0.868 g/ml、門尼粘度ML1+4(121°C)為35的Engage-8150(乙烯-辛烯共聚物,杜邦陶氏彈性體公司生產)。此外,還使用了相對密度為1.9 g/cm3、BET比表面積為120~160 m2/g、粒徑為10~20 nm的沉淀法白炭黑(德國德固賽公司產品)。所使用的過氧化二異丙苯(DCP,美國Aldrich化學公司生產)的純度為98%。另外還使用了發泡劑偶氮二甲酰胺(ADC-21,印度高聚物實驗室生產)。
1.2 試樣制備
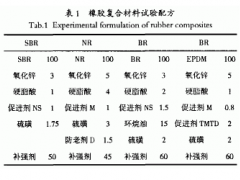
根據膠料配方(見表1),將乙烯-辛烯共聚物與配合劑進行混煉。混煉在帶有凸棱轉子的布拉本德塑性儀(型號為PLE330)內進行。乙烯-辛烯共聚物首先在溫度80°C和轉子速率60 r/min的條件下熔融2 min,爾后加入其他配合劑。連續加入填充劑時,為保證配合劑均勻分散,需再繼續混煉3 min。若是填充膠料,發泡劑應與填充劑同時加入,以獲得較好的分散。最后,加入硫化劑。對膠料進行熱煉,并使其通過小輥距開煉機壓成膠片。用孟山都流變儀R-100測定硫化膠的硫化特性。膠料在壓力為5 MPa的電熱液壓平板硫化機中,以160°C的硫化溫度和以其相應正硫化時間的80%進行硫化。為有利于微孔制品的發泡和易于脫模,使模型各棱邊成30°角。發泡后的微孔膠片在電熱烘箱里以100°C的溫度后硫化1 h。
1.3 動態力學分析
用動態模量儀DDVⅢEP(日本Orientec公司制造),在溫度和應變變化的情況下分析微孔乙烯-辛烯共聚物硫化膠的動態力學性能。試片試驗則在4種頻率(3.5、11、35和110 Hz)下、-100~100°C溫度范圍內,以及0.18%的動態應變條件下進行。為測定與應變有關的動態力學特性,所有試驗均在27±2°C和頻率為11 H的條件下進行。試片長度在整個雙應變振幅(DSA)范圍內從0.083%到5%不等變化。
2 結果與討論
2.1 與溫度有關的動態力學性能
2.1.1 發泡劑的影響
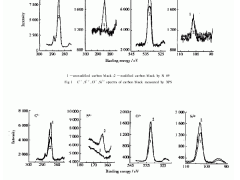
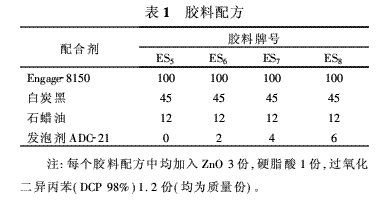
圖1表明,含有不同量發泡劑,并填充45份白炭黑的微孔乙烯-辛烯共聚物硫化膠,其貯能模型E′在11 Hz頻率下對動態力學性能的影響隨溫度的變化而波動。閉孔硫化膠(ES6、ES7、ES8)的貯能模量曲線與密實心硫化膠(ES5)的相似。在玻璃態和橡膠態區域,貯能模量隨發泡劑用量的增加而穩步減少。分解出來的氣體被封閉在閉孔里。閉孔的變形實質上是呈彈性狀的,且對貯能模量的影響較小。因此貯能模量隨發泡劑用量的增加而減少這一現象是由于固體聚合物量減少所致。在4種溫度(-100、-50、50和100°C)條件下,用密實硫化膠和微孔硫化膠的貯能模量分別對密度所作的圖列示于圖2。從對數坐標曲線圖看,線性關系是明顯的。該關系可用下式表示:E′=α×ρb該式中,ρ為密度,a和b分別為與溫度有關的常數。
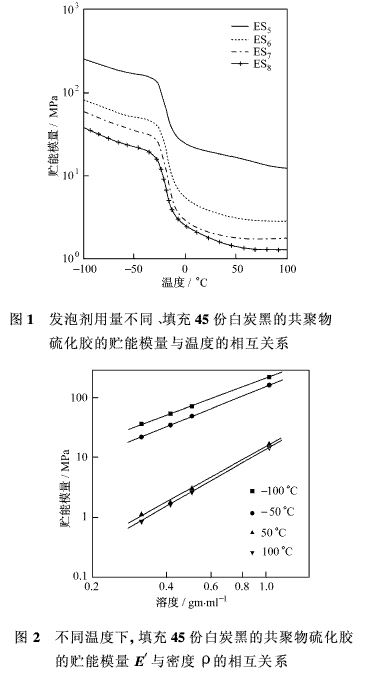
在曲線圖里,b為直線斜率,在-100、-50、50和100°C溫度下,其值分別為1.58、1.72、2.32和2.41。這表明,在較高溫度下,貯能模量隨密度的減少而降低的量比低溫時的要小。圖3為填充45份白炭黑的密實硫化膠和微孔硫化膠在4種不同溫度下,其相對貯能模量(E′f/E′s)對相對密度(Pf/Ps)所作的圖。在所有溫度下,當相對密度減小時,相對貯能模量亦減小。從這些數值看,在任何特定的相對密度下,當溫度增加時,閉孔硫化膠的相對貯能模量明顯較低。填充45份白炭黑的密實和微孔硫化膠的tanδ值隨溫度波動的情況見圖4。該圖表明,硫化膠的減振性能隨發泡劑用量的不同而各異。β轉化值為初始松弛,并被認為是由受束縛的非結晶鏈段的玻璃化轉變溫度引起的,與特定歷程無關。β松弛與非晶相有關,其效果與低結晶聚合物里的玻璃化溫度相同。相當于玻璃化轉變溫度(Tg)的β轉化值列于表2。
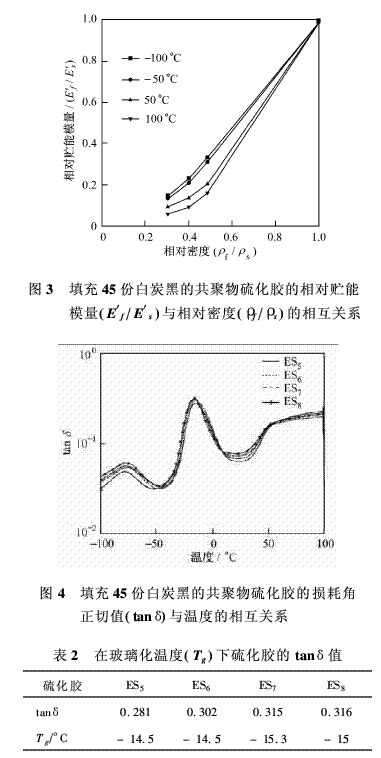
在橡膠態區域,當發泡劑用量增至4份時,tanδ值減小;而后增至6份時,該值增大。封閉于閉孔里的氣體對減振性能的影響較小。就含有較多量發泡劑的閉孔硫化膠而言,從閉孔里分解出來的氣體壓力增加,使孔壁產生應力。因此,孔壁處于應變狀態下。應變增加到一定程度時,tanδ值便增大。
2.1.2 頻率的影響
圖5a和5b為填充45份白炭黑的密實硫化膠和加入2份發泡劑的微孔硫化膠的logE′對logf所作的圖。加入4份發泡劑和6份發泡劑的硫化膠的曲線類似。這些圖給出了硫化膠在3.5、11、35和110 Hz 4種頻率下和溫度30~100°C范圍內變化時的貯能模量值。可見該模量值與應變速率有關,且在各種溫度下隨頻率的增加而增加。從中亦可看出,當溫度升高時,貯能模量隨頻率和直線斜率的增大而呈線性變化。在該分析過程中,為產生疊加效應,取30°C作為參考溫度,將直線沿f軸移動。用如此獲得的合成移動系數logαT對103/T所作的圖示于圖6。根據直線斜率,用Arrhenius方程式計算ΔH值。
logαT=ΔH/2.303R(1/T-1/T0)該式中,T0=303 K,αT為移動系數,ΔH為活化能,R為氣體常數。
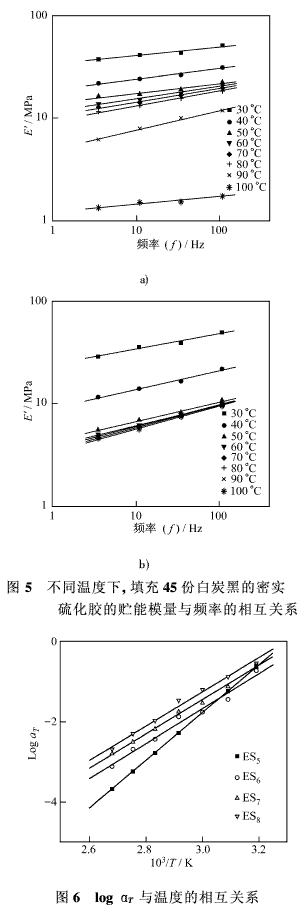
密實硫化膠的活化能為27.18 kcal/mol。而分別加入2、4和6份發泡劑的微孔硫化膠的活化能分別為20.28 kcal/mol、18.72 kcal/mol和17.08 kcal/mol。由此可看出,ΔH與密度有關。為畫出總的曲線圖(圖7),可將獲得的ΔH值代入方程式(2),計算logαT值。加入2份發泡劑的硫化膠在3.5、11、35和110 Hz頻率下,tanδ對溫度所作的圖示于圖8。在橡膠態區域,tanδ值隨頻率的減小而減小。Tg隨頻率的增大而降低,且有偏向于較高溫度一側的趨勢。
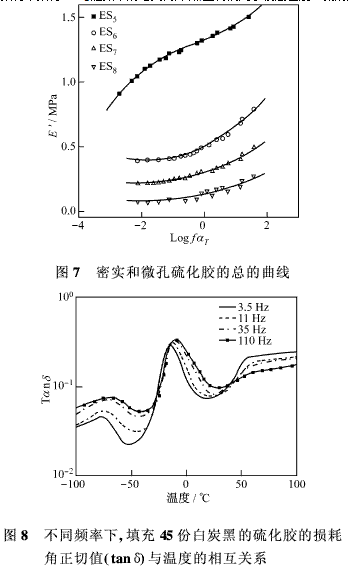
2.2 與應變有關的動態力學性能
2.2.1 貯能模量
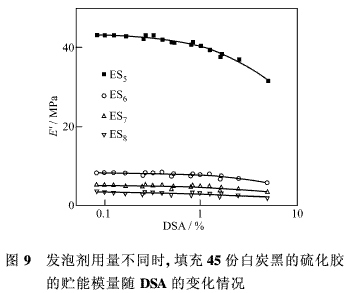
圖9說明了填充45份白炭黑的密實和微孔硫化膠,其應變和發泡劑用量對貯能模量的影響。在最小的應變振幅下,密實和閉孔兩種硫化膠均顯示出最大的貯能模量(E′)。在最小的DSA下,三維的填充劑-填充劑、填充劑-聚合物和殘存在閉孔里的空氣對所產生的應變起著剛性件的作用,從而表現出最大的E′值。在該網絡結構中,較小的應變不可能產生任何重大的變化。貯能模量隨應變的增大而減小。在密實硫化膠中,貯能模量隨應變減小的量比微孔硫化膠中更為明顯。從圖中可以看出,硫化膠對1%以下的應變的影響并不敏感。但是,隨著發泡劑用量增加,貯能模量卻急劇降低。由于發泡劑用量增加,孔壁厚度和硫化膠的剛性度均減小,從而導致貯能模量降低。DSA大于1%時,貯能模量隨著應變的增加而大幅度下降。這可歸因于挺性較差的孔壁在應變振幅增大時塌陷了。
2.2.2 損耗角正切值
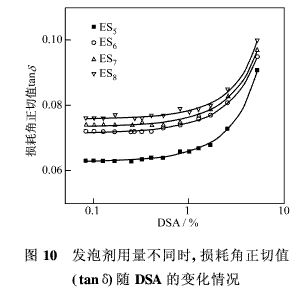
圖10為填充45份白炭黑的密實和微孔硫化膠的tanδ對DSA所作的圖。由該圖可看出,tanδ值隨發泡劑用量的增加而增大。此外,tanδ值還隨應變的增加也略有增大,到DSA達到1%時,其增大的速率陡然上升。tanδ值隨發泡劑用量的增加而增大是由于大量氣孔生成和孔壁厚度減小所致。在閉孔硫化膠中,孔壁的彎曲、皺縮和伸長在低應變條件下產生,因而其tanδ值比相應的密實硫化膠的高。在應變較大時,密實硫化膠的tanδ值增大是由于填充劑聚集破壞所致。若是微孔硫化膠,除上述原因外,氣孔倒塞和塌陷均會對較大的tanδ值有影響。
2.2.3 E′與E″的關系
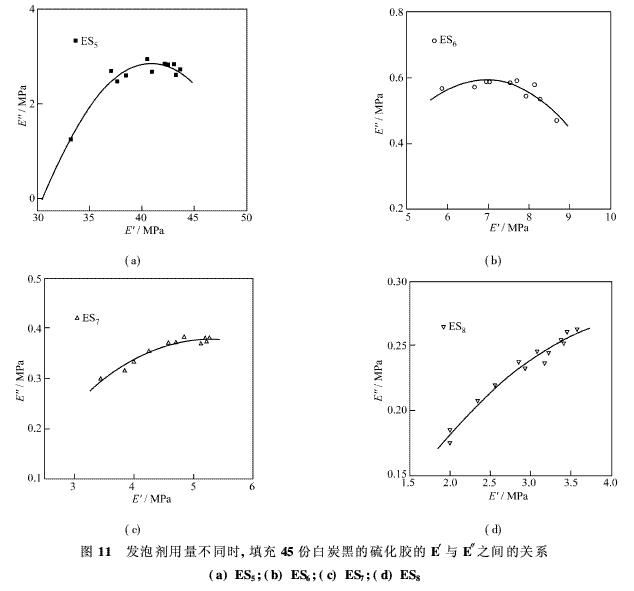
就密實和微孔硫化膠而言,其E′與E″之間的關系被列示于圖11。圖中圓弧上的各點均代表不同的振幅。由(a)(b)(c)(d)四圖比較可見,圓弧線隨發泡劑用量的增加而縮短。在較小的振幅下,貯能模量由于閉孔硫化膠孔壁的彈性皺縮或伸長而出現較大值。因某些孔壁在較大的振幅下會破損,故其貯能和損耗兩種模量均減小,這與圓弧關系相一致。
2.2.4 tanδ與E′的關系在10%DSA和25°C溫度條件下,天然膠的tanδ與模量的簡單關系式如下:
tanδ= 0.033+0.0449[E1%-E10%]1/2
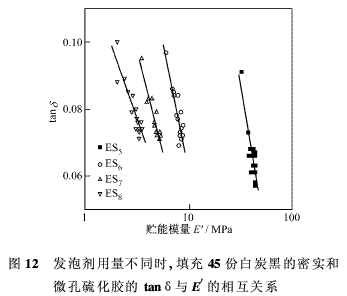
填充炭黑的EPDM硫化膠的tanδ和logE之間的線性關系也已建立。圖12為填充45份白炭黑和含不同用量發泡劑的密實和閉孔硫化膠的tanδ值對logE′所作的圖。該圖的線性性質可表示為:
tanδ=mlogE′+C1
式中,m為直線斜率,C1為常數由于發泡劑的加入,斜率m上升,而常數C1值較之密實硫化膠相應的值小。
2.2.5 滯后損失與應變功
滯后損失是硫化膠正弦變化時的能量損耗。它被定義為:
H=Ws×sinδ,而Ws=π/4[DSA]2×E*
式中,H為滯后損失,WS為應變功,E*為復合模量。
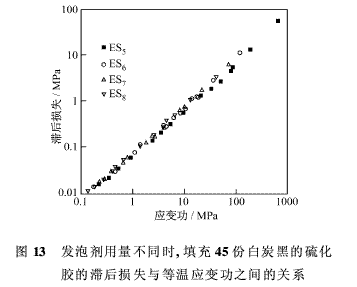
雖然建立了上述定義,但所測定的參數之間的真正關系可通過logH對logWs作圖來確定。圖13說明了這種線性關系。該關系滿足下列方程的要求:
lnH= lnH0+mlnws,即H=Wms×H0
當發泡劑用量增加時,m值從1.016減少到1.014,而H0的值卻從0.062增大到0.078。
3 結論[1]
(1)微孔乙烯-辛烯共聚物硫化膠的貯能模量(E′)或剛性度隨發泡劑用量的增加而降低。就密度而言,在各種溫度下,貯能模量的log-log圖呈線性關系。溫度升高時,直線的斜率增大,即貯能模量降低的速率隨密度的減小而提高。
(2)相對貯能模量(Ef/Es)隨相對密度(ρf/ρs)的減少而降低。在任何相對密度下,當溫度升高時,相對貯能模量均降低。
(3)在玻璃態區域,tanδ值隨發泡劑用量的增加而增大。但在橡膠態區域,當發泡劑用量達到4份時,tanδ值反而減少。發泡劑用量增至6份時,tanδ值卻又增大。
(4)貯能模量被證實與頻率有關。頻率增加時,貯能模量在所有溫度下均提高。對于密實和微孔硫化膠,可使用由Arrhenius方程計算出來的移動系數,并借助于時間-溫度疊加原理來繪制模量對log(減小的應變速率)的總曲線。活化能被證實與密度有關。
(5)在橡膠態區域,tanδ隨頻率的減小而減小。但在40°C以上時,該值隨頻率的增大而減小。當頻率增加時,Tg減小,且有向較高溫度一側偏移的傾向。
(6)應變較小時,貯能模量隨發泡劑用量的增加而降低。應變大于1%時,密實硫化膠貯能模量的下降速率比微孔硫化膠的更快。但是,損耗角正切值的趨勢卻與此相反。
(7)E′對E″所作的圖呈弧線形,且圓弧隨發泡劑用量的增加而縮短。
(8) tanδ值與E′之間的關系,以及滯后損失和應變功被證實是線性的。
參考文獻:
[1] N. C. Nayak, D. K. Tripathy. Silica-filled closed-cell microcellular[J]. Kautschuk Gummi Kunststoffe,2005, 58(1-2):50-54.